After a PhD in pure mathematics, Charlotte Wahl now holds a position at the Leibniz Archive in Hannover, where she edits the mathematical writings and correspondences of the great mathematician. In this interview, she tells us about her work in the history of mathematics and index theory, about the pleasures and privileges of having a glimpse into Leibniz’s work and life, and of course about the famous dispute with Newton. Interview by Francesca Arici and Anna Maria Cherubini.

Can you tell us more about the Leibniz library and the Leibniz Archive?

One has to differentiate between the Leibniz edition and the Leibniz Library. I work at the Leibniz Archive, which is a department of the Leibniz Library. The Leibniz Library is where the estate of Leibniz is stored.

Our offices are in the building of the Leibniz Library but our group in Hannover is only one part of the Leibniz edition, which is located in four different cities in Germany. There is a group in Münster which deals with philosophy: with Leibniz’s philosophical writings and correspondences. There is a group in Potsdam which deals with Leibniz’s political writings and there is a group in Berlin which deals with Leibniz’s writings in the natural sciences and medicine.

Who is funding the Leibniz library and the Leibniz archive?

The Leibniz edition is a long-term project of the Göttingen and Berlin academies of sciences. These projects are funded by the states (in our case Niedersachsen, Berlin and Brandenburg) and by the federal government.

What is the focus of your group?

We focus on writings and correspondences. We are in charge of all the writings in mathematics and of all correspondences besides the ones in philosophy: this leaves us with mathematics, natural sciences, history and politics.

Who was Leibniz corresponding with, just to get an idea?

There are many famous mathematicians of course, like the Bernoulli brothers. Leibniz was in contact with Jacob Bernoulli, who worked in stochastics and found the law of large numbers, and with his brother Johann. He also wrote letters to the marquis de l‘Hôpital and to John Wallis, who was a famous mathematician at the time. There is also a very short correspondence with Newton, that’s famous!

Have you developed a personal opinion about the famous Newton—Leibniz dispute?

I actually did some research on this. From our perspective, there is still a lot to discover because Leibniz died in 1716 and the dispute began in the last five years of his life. We are still editing the correspondences of that time. Many of them haven’t been published and haven’t been researched yet. My opinion is that Leibniz and Newton got along for a long time. They didn’t have so much contact with each other but they were behaving respectfully towards each other until about 1710, so for almost 40 years. Then the dispute began and it became very nasty very quickly. Other people, however, are of the opinion that the dispute had been there already since 1676. So this is the relevant question at the moment: what was their relationship like between 1676 and 1710? Was there some hidden animosity already from the beginning? This is what we are trying to understand.

How does it feel to have access to the writings of Leibniz? Can you get a glimpse of his personality?

One gets a very good idea of the man behind the pen. There about 20.000 letters that we have access to, including those from his correspondents. One gets quite a good picture of his personality by reading those letters, though it wasn’t really customary at that time to expose one’s emotions in their letters.

There were lots of conflicts at the time, also between scientists. For example, there was a big conflict between the Bernoulli brothers, so that at some point they were real enemies. 

Leibniz was a big mediator, always trying to find some compromise between people who were in conflict. He liked intellectual controversies but he didn’t like it when they became too personal…

Are there also letters that sound more personal? Did he develop some friendship with his correspondents?

First of all, one must say that with many of his correspondents he never met. They called each other friends, but friendship clearly had a different meaning than it has today. What they also did were services to each other. For instance, in the Netherlands there was a very liberal book market at the time, so Johann Bernoulli organised to publish an anonymous political pamphlet for Leibniz, which Leibniz would not have been able to publish in Germany.

The letters also contain some more personal remarks. For instance, Leibniz was in very good terms with the Duchesses, like Sophie Charlotte von Brandenburg and Sophie von Hannover. When Sophie Charlotte von Brandenburg died in 1705 at quite a young age, Leibniz was very affected by this event. For about half a year he was very sad and didn’t write so many letters and this sadness transpired in many of his writings of the time. In several letters, he mentioned how much he had liked to talk to her, and how big a loss her death was for him. These are the sort of remarks one can find in these letters. Of course one also finds announcements concerning events like the birth of a new child and so on.

Quite strangely for us, when they are ill his correspondents sometimes describe in great detail the symptoms of their illnesses, something we would not really do today. The feeling I get is that they were helpless towards their illnesses: their limited medical knowledge made it that they never knew whether they would survive, so they documented what was happening to them.

Is your approach to the study of this collection of letters centred around the figure of Leibniz? Or are you seeing his work as part of something bigger?

There is a big project in Oxford, and there are many more around Europe and the United States, where the way correspondences are represented is not around one single person, like for instance Leibniz, but in a network that connects the various correspondents. We also contribute to some of these projects. Last year I attended a workshop in Wolfenbüttel on the correspondences of Leibniz and his networks. Examples of this are his contacts to the Jesuits. I personally have worked on and talked about Leibniz’s network with astronomers.

What role does modern technology play in your studies?

We are also involved with a project, done in collaboration with MusterFabrik Berlin, where we scan and try to reconstruct Leibniz sketches. We are using a technique that the Fraunhofer Institute in Berlin developed to reconstruct and study the STASI Akten.

At Leibniz’s time, paper was extremely expensive. So after writing down or sketching an idea on paper, he would cut it to save the part of the sheet that was empty, to be later able to use it for some other idea. The result is that we are now in possession of small pieces of papers with no date on them. If we want to edit them, we have to find a chronology. This program we are using tries to reconstruct the whole piece of paper so one knows that all these small pieces belonging to the big puzzle had very likely been written around the same time. The hope is that we can find a date for one of the pieces: for instance, one piece could be a letter, or there could be some external evidence useful for dating.

We had some success so far, and in the future, we would like to use the letters of our archive as well. Leibniz’s estate is really big, about 100.000 folios. For now, the method has been used on a small part of the estate, that belongs mostly to the mathematical writings. Some puzzles have been successfully reconstructed. The letters have not been used yet, because at the moment there is really too much data to be processed. Most of this material is in our library and we are looking into funding to develop this further to include all the letters and other writings.

Gottfried Wilhelm Leibniz

What is so special about the estate?

The good thing about the estate is that very little is lost and it is nearly all in Hannover. This is unique about this estate. Also, Leibniz threw very little away, for example, we have nearly all the letters he got from his correspondents. This is also why this collection became UNESCO documentary heritage.

What made sure that the estate was so well preserved?

Leibniz was a state employee. he had a position at the court in Hanover (Geheimer Justizrat). When someone in such a position died, his belongings were often confiscated by the state to check them for interna. Since his correspondence and writings were so vast they could not be checked immediately, so they stayed at the court library — essentially where they were from the start because Leibniz was also the court librarian and the library was in his house. Our library is the former court library, so in some sense, we are the successors of Leibniz. The material just stayed there for all these centuries.

Setting Leibniz aside now, we would like to find out more about you. How would you describe your career path?

I did pure maths until my PhD in Göttingen. Ulrich Bunke (now in Regensburg) was both my Diploma and PhD supervisor. After my PhD I was a postdoc in Paris and later at Virginia Tech. I had done a lot of things during my studies aside maths, I had learned languages, taken lectures in philosophy… Unfortunately, there is not a lot of history of mathematics in Germany, but there were some lectures in Göttingen, which I followed, too. In some sense, I wanted to do something between mathematics and the humanities. When I came back from my postdocs I had decided that I wanted to leave the academic career because it is so difficult to get a permanent position. I thought I really wanted to have some job security and I dislike the feeling of going on for years without knowing where I would end up. And I was happy I could find something between the humanities and mathematics. Of course it was sort of a coincidence because the position was free at the right time and at the beginning it was a 9-month position only, I was really lucky because there were not so many people applying for this position. I had no degree in history of mathematics but the call said mathematicians could apply too because what you really need is knowing mathematics and being able to read French and Latin.

How did you end up studying mathematics, given your passion for the humanities?

Actually, I started with physics but then I switched pretty soon. When I was following a mathematics course in the physics program, I thought everything was being done too sloppily… It’s true that when I was young I was really interested in many things but one has to start with something. I chose physics and mathematics because they are in some sense the foundation of everything and then I thought perhaps I might go on later, but this, of course, didn’t happen. After my PhD I had to decide whether to stay in academia or look for something else and then I reached a decision and this is how I ended up where I am now.

How would you explain your mathematical work to a non-expert?

I wrote my dissertation on the heat equation on a very particular geometric object one might call the octopus surface. This is actually easy to explain even to non-mathematicians: I basically studied how heat propagates in an octopus…

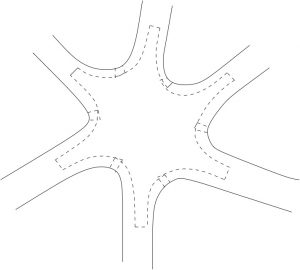
The Octopus Surface

One can think of the octopus surface as being made out of sheets of paper (with some curvature in the middle) and having infinitely long legs.  It is an infinite manifold and also has a boundary. These are the main characteristics. I studied a particular invariant, an index, and this turned out to have a geometric meaning since it equals the Maslov index in symplectic geometry. This is constructed as an index of a Dirac operator with special boundary conditions given by Lagrangians. This was done by Bunke earlier in the classical case, and I studied the same problem in the noncommutative setting. This means that, for instance, a Lagrangian subspace is replaced by a submodule in some larger C*-module. As a result, one gets a noncommutative generalisation of the Maslov index, and to study its properties was the motivation behind my project. 

What I really liked about index theory is that one gets topological data out of analytical objects, so it establishes a connection between different fields within mathematics.

What are your passions, aside mathematics and the history of mathematics?

Like many mathematicians I play music. I play the violin and the piano and I also sing in a choir. We recently performed the Johannespassion by Bach.

Do you have a dream, a big project or a mathematical question you would like to answer?

I have quite some small unfinished projects. I would love to write a book, but for that, I need to find the right opportunity. From time to time I write articles about mathematics and I write articles about Leibniz and the history of mathematics. So I am still doing mathematics and I am very happy about this combination. Though I do not have so much time for maths anymore, it suits me very well. I take big breaks where I do not do mathematics for a couple of months, and then I rethink about a problem and often I realise I have solved it in the meantime. I don’t know how it happens, maybe I continued to work on it subconsciously. So it works better for me than doing mathematics on an everyday basis, where you are so absorbed in the details that you do not see the big picture anymore.